Finding compelling slices of global markets to overweight isn’t getting any easier. After an extended run higher in much of the world’s risk assets, the low-hanging fruit has been picked. But there’s always relatively attractive markets. All the usual caveats apply, of course, but beggars can’t be choosy.
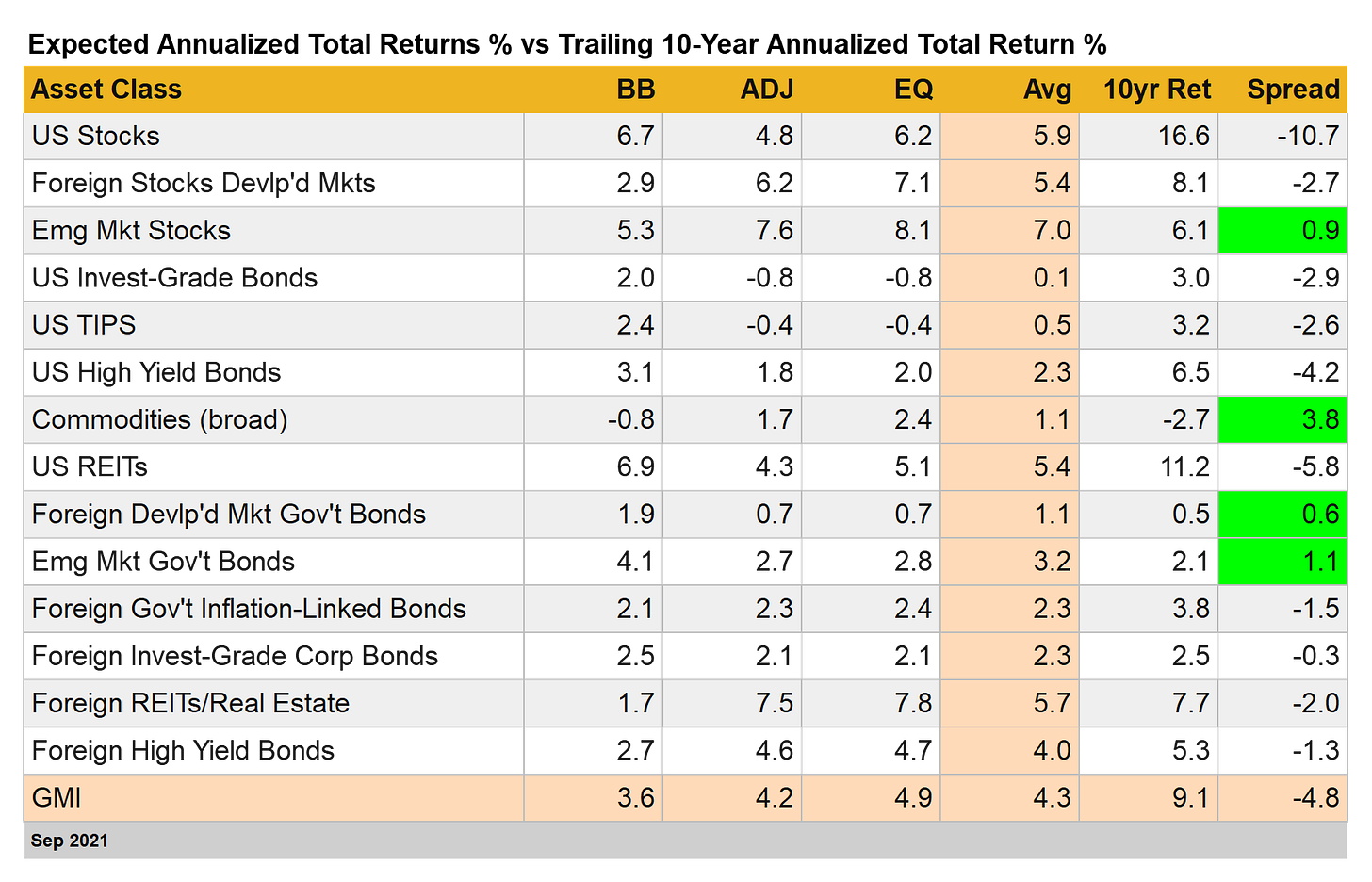
As an example, consider a new column of data — Spread — that’s now part of the periodic return estimates for the major asset classes on these pages (see this introduction for background). The basic idea is the new addition to the numbers is to identify markets with trailing 10-year returns that deviate substantially from the performance forecasts (based on averaging three models, which are defined below). The logic: If asset x has a trailing return substantially below the expected return, there’s a case for overweighting (and vice versa).
Is this a flawless strategy that will quickly and reliably generate unusually high returns? Uh, no. And there’s no tooth fairy either. But looking at these divergences offers a basis for deciding where a closer look is warranted for adjusting portfolio weights.
That brings us to the table below (which crunches data through Sep. 2021). The positive spreads (expected return above 10-year trailing return) are in the minority these days (highlighted in green). The biggest positive spread is found in commodities, which are posting a trailing annualized 10-year loss of 2.7% vs. an expected long-term performance of 1.1% — that translates to +3.8 percentage points.
The next-highest spread is in emerging markets government bonds with a +1.1 percentage point spread.
Another way to use the spread data is to identify the deepest negative readings. That honor goes to to US stocks, which have a deeply negative 10.7 percentage-point chasm. Ouch! The implication: the sizzling 16.6% annualized total returns for American shares over the past decade is lofty in the extreme vs. the 5.9% annualized expected return (via the model average). That doesn’t mean we should avoid US stocks entirely (extremes are rarely productive in asset allocation). But it’s a reason to at least consider lightening up on the allocation, particularly if a portfolio is substantially overweight in this corner, which is likely after the latest bull run in US stocks.
Finally, here are brief definitions for the table above:
BB: The Building Block model uses historical returns as a proxy for estimating the future. The sample period used starts in January 1998 (the earliest available date for all the asset classes listed above). The procedure is to calculate the risk premium for each asset class, compute the annualized return and then add an expected risk-free rate to generate a total return forecast. For the expected risk-free rate, we’re using the latest yield (for the target month, which is July 2021 in this case) on the 10-year Treasury Inflation Protected Security (TIPS). This yield is considered a market estimate of a risk-free, real (inflation-adjusted) return for a “safe” asset. Note that the BB model used here is (loosely) based on a methodology originally outlined by Ibbotson Associates.
EQ: The Equilibrium model reverse engineers expected return by way of risk. Rather than trying to predict return directly, this model relies on the somewhat more reliable framework of using risk metrics to estimate future performance. The process is relatively robust in the sense that forecasting risk is slightly easier than projecting return. The three inputs:
An estimate of the overall portfolio’s expected market price of risk, defined as the Sharpe ratio, which is the ratio of risk premia to volatility (standard deviation). Note: the “portfolio” here and throughout is defined as GMI
The expected volatility (standard deviation) of each asset (GMI’s market components)
The expected correlation for each asset relative to the portfolio (GMI)
This model for estimating equilibrium returns was initially outlined in a 1974 paper by Professor Bill Sharpe. For a summary, see Gary Brinson’s explanation in Chapter 3 of The Portable MBA in Investment. I also review the model in my book Dynamic Asset Allocation. Note that this methodology initially estimate risk premium and then adds an expected risk-free rate to arrive at total return forecasts. The expected risk-free rate is outlined in BB above.
ADJ: This methodology is identical to the Equilibrium model (EQ) outlined above with one exception: the forecasts are adjusted based on short-term momentum and longer-term mean reversion factors. Momentum is defined as the current price relative to the trailing 12-month moving average. The mean reversion factor is estimated as the current price relative to the trailing 60-month (5-year) moving average. The equilibrium forecasts are adjusted based on current prices relative to the 12-month and 60-month moving averages. If current prices are above (below) the moving averages, the unadjusted risk premia estimates are decreased (increased). The formula for adjustment is simply taking the inverse of the average of the current price to the two moving averages. For example: if an asset class’s current price is 10% above its 12-month moving average and 20% over its 60-month moving average, the unadjusted forecast is reduced by 15% (the average of 10% and 20%). The logic here is that when prices are relatively high vs. recent history, the equilibrium forecasts are reduced. On the flip side, when prices are relatively low vs. recent history, the equilibrium forecasts are increased.
Avg: This column is a simple average of the three forecasts for each row (asset class)
10yr Ret: For perspective on actual returns, this column shows the trailing 10-year annualized total return for the asset classes through the current target month (July 2021 in this case).
Spread: Trailing 10-year return less model-average forecast. ■